The design and selection of reactors to evaluate catalyst candidates at the laboratory scale is critical to success at industrial scale
![Figure 1. A typical catalyst pellet is composed of porous particles (adapted from [2])](https://www.chemengonline.com/wp-content/uploads/2015/03/19.jpg)
Figure 1. A typical catalyst pellet is composed of porous particles (adapted from [2])
This article focuses on the elements that govern the choice of a laboratory catalytic reactor for experimental studies as well as a brief description of the different catalytic reactors that are available for catalytic studies. The article includes definitions of some of the most frequently encountered terms in heterogeneous catalysis. Basic criteria and guidelines are also given for selection of laboratory reactors. This how-to primer focuses on the following areas of catalyst testing and development in laboratory and bench-scale catalytic reactors:
What are some of the measures of specific reaction rates and reactivity for experimental catalysts? What are the basic choices of ideal flow reactors available for kinetic runs in the laboratory? How to ensure the absence of intraparticle and extraparticle transport (mass and heat) limitations (by use of diagnostic and mathematical criteria) so that the experiments are carried out under kinetic control? What are some of the experimental diagnostic tests for intraparticle and extraparticle gradients?
Basic terms and definitions:
A typical supported metal catalyst (Figure 1) consists of metal nanoparticles (on the order 1-20 nm) distributed throughout the pore structure of a frequently inert inorganic support [2]. The metal particles can be tailored to reside at the exterior of the pore structure of each support particle or can be tailored to be at the center of the pore structure. These catalysts are termed “eggshell” or “cherry” catalysts, respectively. The distribution of the active metal inside the catalyst pellet (which itself is a morph of several individual submicron-sized particles, each consisting of a complex architecture of interpenetrating pore networks) can take several forms, as shown in Figure 2. The most common of these are eggshell catalysts (Figure 2b), where the active metal is dispersed on the exterior of the pellet and the egg-yolk (also termed cherry, Figure 2d) catalyst, where the active metal resides at the center of the pellet. The other two types are uniform (Figure 2a) where the active metal is distributed uniformly throughout the pellet, and the egg white (Figure 2c), where the active metal forms the egg-white feature of the pellet, and can be distributed uniformly in the egg-white (the region other than the egg-yolk) region.
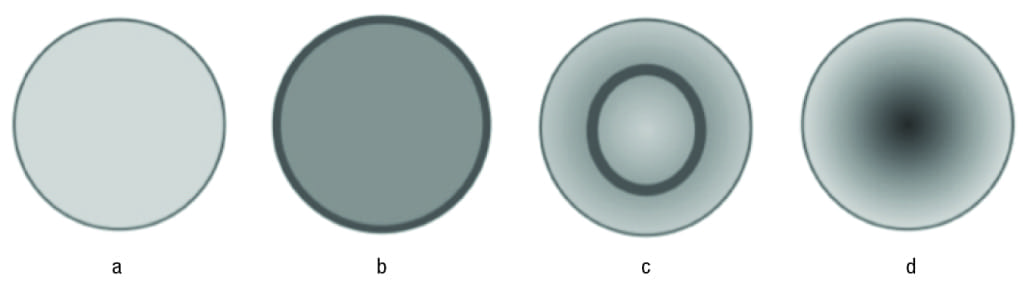
Figure 2. There are several possible distributions of active component in a catalyst pellet: (a) uniform; (b) egg-shell; (c) egg-white; and (d) egg-yolk
The support particles are porous, and contain pores in the three basic size ranges. Pores in the size range of 2-5 nm are called micropores, those in the size range of 5-50 nm are called mesopores, and pores greater than 50 nm are known as macropores.
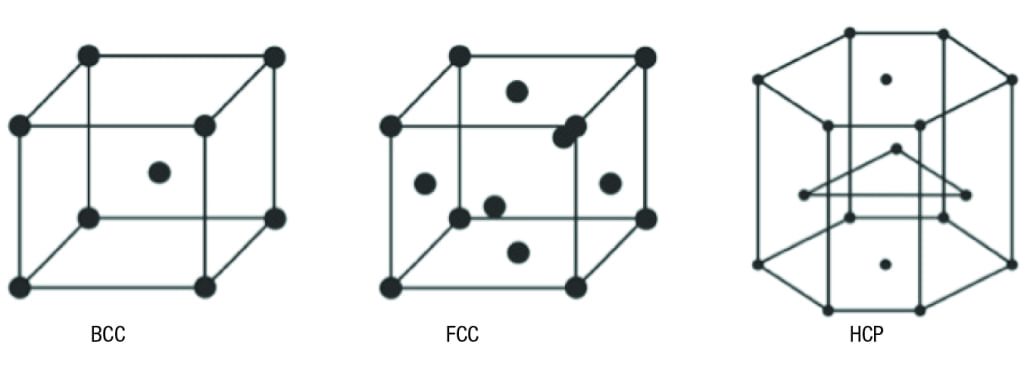
Typical supported metals are different than single crystals, which are crystals that can be cut and processed to expose various surface crystal planes. The crystal structures which are pertinent from the standpoint of catalytic chemistry are the body-centered cubic, face-centered cubic, and hexagonal structures (Figure 3).
Figure 3. The BCC, FCC and HCP crystal structures are shown here
Apart from supported metals and single crystals, other categories of heterogeneous catalysts are encountered in the literature. These include zeolites, metal oxides, mixed metal oxides, sulfides (typical hydrotreating catalysts), and materials such as nitrides, phosphides and carbides. There are more novel materials in the literature that include the aluminophosphates (AlPO’s), silicoaluminophosphates (SAPO’s), MCM series, metal organic frameworks (MOF), and biologically-inspired materials, including biomimetics. These novel materials are currently of mostly laboratory interest only.
The surface area, pore volume, and pore size distribution are important textural features of a supported-metal catalyst. The first property, surface area, is measured using physical adsorption of a suitable adsorbate, most typically N2, at the liquid nitrogen temperature of 77K, and the adsorption isotherm is analyzed using the BET (Brunauer, Emmett, and Teller) method. In a landmark contribution, the three proposed a model for multilayer adsorption and arrived at an equation describing it that allows for the calculation of monolayer coverage of the adsorbate, as in Equation (2). The resultant surface area is therefore called the BET-N2 surface area. There are two common methods for the measurement of pore volume and pore size distribution of solid porous catalysts. The first, called the Hg porosimetry method, is used for larger pores (above 10 nm). To determine the distribution of pores with diameters smaller than about 20 nm, a nitrogen desorption method is used that uses the Kelvin equation to relate the pore radius to ambient pressure.
While the overall surface area is important, often more crucial in catalytic science is the active metal surface area. Concomitantly, while the bulk loading of the metal is important, more important from the standpoint of catalytic reactions is the metal dispersion. The metal dispersion is a ratio of surface metal atoms to the total metal atoms [2]. The metal particle size is usually calculated from dispersion, and is simply the size (in nm) of the metal cluster. The metal particle size and the particle size distribution is directly measured using high-resolution transmission electron microscopy (HRTEM in bright and/or dark fields) or powder X-ray diffraction (PXRD), or is indirectly measured using titration of the surface atoms using probe molecules such as H2, CO, or O2, as in chemisorption measurements. Other tools based on temperature-programmed methods and spectroscopy also are invaluable in physicochemical characterization.
Catalyst performance measures
Frequently, in a typical experiment, the reactants in the gas phase are contacted with a fixed catalyst charge (say, in a differential fixed-bed reactor system), at specified conditions of temperature, pressure and space velocity (defined as volumes of gas at normal temperature and pressure conditions per unit volume or unit mass of the catalyst charge per unit time). Catalyst performance features, including conversion, selectivity, yield, specific reaction rates, areal reaction rates and turnover frequencies, are assessed.
Conversion, selectivity and yield. The conversion, selectivity and yield are defined as follows, for a simple chemical reaction:
A + B —> C + D (1)
Let A be the limiting reactant and let NA0 be the number of moles of (limiting) reactant A fed to the reactor inlet (NB0 is the number of moles of reactant B). C is the desired product, and NC is the number of moles of product C. The total moles of product are then NC + ND = NP.
Conversion(%) = [(NA0 – NA) / NA0] x 100 (2)
Selectivity of product C (%) = [NC /(NC + ND)] x 100 (3)
Yield of product C (%) = NC / NA0 x 100 (4)
Specific reaction rate and turnover frequency. The specific reaction rate can be defined on the basis of catalyst particle volume or mass (or, bed volume or mass), and the areal rate is frequently defined on the basis of overall surface area or the metal surface area. The turnover frequency (TOF) is a very important performance feature because it enables comparison of data obtained on similar reactions and catalysts in different experimental tests and laboratories. TOF is defined as molecules of reactant or product per surface metal atom per second, and has the units of sec -1. Thus TOFs (or areal rates, rates based on active metal surface areas) must be reported whenever possible in any proper catalytic study.
A balance between transport rates of reactants (to and from the catalyst surface, or the active site) and chemical reaction rates is the proper way to operate a commercial reactor. This is frequently called as the Weisz window for commercial operation, and is quantified to be 1µmol/cm 3·s. This reaction rate translates into a TOF of 1 s -1, for many catalysts. However, for laboratory reactors, the TOF values are frequently 1 to 2 orders of magnitude lower than the value for commercial operation, as diffusion and transport do not play a role in surface reaction kinetics. This mode of operation is referred to as kinetic control, and is used on the laboratory scale for estimation of intrinsic kinetics of catalytic reactions [11]. A simple definition of TOF can be given as follows:
TOF(s -1) = [rate of reaction (mol/g catalyst· s) / catalyst loading (g metal/g cat)] × [(atomic weight of metal (g metal/mol) / fraction of total metal atoms that are on surface] (5)
In the previous formula, the catalyst loading (g metal/g catalyst) is the experimental loading, determined using a tool such as inductively coupled plasma — optical emission spectroscopy (ICP-OES) or inductively coupled plasma — mass spectrometry (ICP-MS).
Some basic guidelines for proper collection and analysis of reaction rates in terms of TOFs are as follows [12,13]:
TOF data should be collected under surface-reaction control. That is, in the absence of extraparticle and intraparticle heat and mass transport limitations TOF and kinetic data should be collected in the absence of deactivation effects due to poisoning, coking or sintering TOF data should be collected over wide ranges of temperature and partial pressures (of reactants) to enable easy comparison with data from other laboratories For structure-sensitive reactions, (those reactions where the TOF is a function of the surface structure and the crystallite size) these effects of metal dispersion and crystallite size should be taken into account.
Apparent reaction orders and activation energy. A key consideration in the experimental catalytic science is the determination of reaction orders with respect to reactants and the apparent activation energies of the reaction. Frequently, in gas-solid reactions, the TOF is modeled as a function of the partial pressures (or concentrations) of the reactants. Consider the synthesis of ethanol (and light alcohols) from synthesis gas (with a H2-to-CO ratio of 1) over a 2%Rh/2.5%Fe/TiO2 catalyst, in a fixed-bed microreactor system, at nominal conditions of 543K and 20 atm. The overall reaction can be written as:
2CO + 4H2 —> C2H5OH + H2O
ΔH o (298K) = –253.6 KJ/mol (6)
The reaction is thus highly exothermic. One approach to determining the activation energies and reaction orders with respect to H2 and CO is from the plots of ln(TOF) versus 1/T and from plots of ln(TOF) versus ln(pCO) or ln(pH2). Frequently, in such cases, an inert gas such as He or Ar is used to dilute the feed, and the partial pressure of one of the reactants is varied while the other is held constant. For example, one strategy to determine the apparent reaction order with respect to H2 is to hold the partial pressure of CO constant at, say, 2 atm, and change the partial pressure of H2. The partial pressure of the inert gas will change as well, to make up the total pressure to a nominal 20 atm.
Dispersion and metal particle size. The final term, dispersion, is the fraction of the total metal atoms that are on the surface (these are considered to be active sites). As stated previously, dispersion is frequently determined using surface titration of metal atoms using probe molecules such as H2, CO, or O2, and is called chemisorption. For most metals, a simple empirical relationship exists between metal particle size and dispersion, as:
dp = 1.1/D (7)
where:
dp = particle diameter (assuming spherical particles)
D = dispersion, the fraction of total metal atoms that are on the surface of the metal
A detailed discussion of the several methods for the collection and analysis of laboratory data is available in many recent works [14-18] and is not included here.
Guidelines for catalyst testing
This section addresses the elements of a proper selection and design of a laboratory catalytic reactor. Frequently, in a typical laboratory experiment, the reactants in the gas phase are contacted with a fixed catalyst charge (for example, in a differential fixed-bed reactor system), at specified conditions of temperature, pressure and space velocity, and the catalyst performance metrics including conversion, selectivity, yield, specific reaction rate, areal rate and TOF are assessed.
The basic considerations in a catalyst testing program are as follows [12,19]:
- Select appropriate laboratory reactor
- Establish ideal flow pattern
- Ensure isothermal operation
- Diagnose and minimize transport disguises
- Assess catalyst stability early
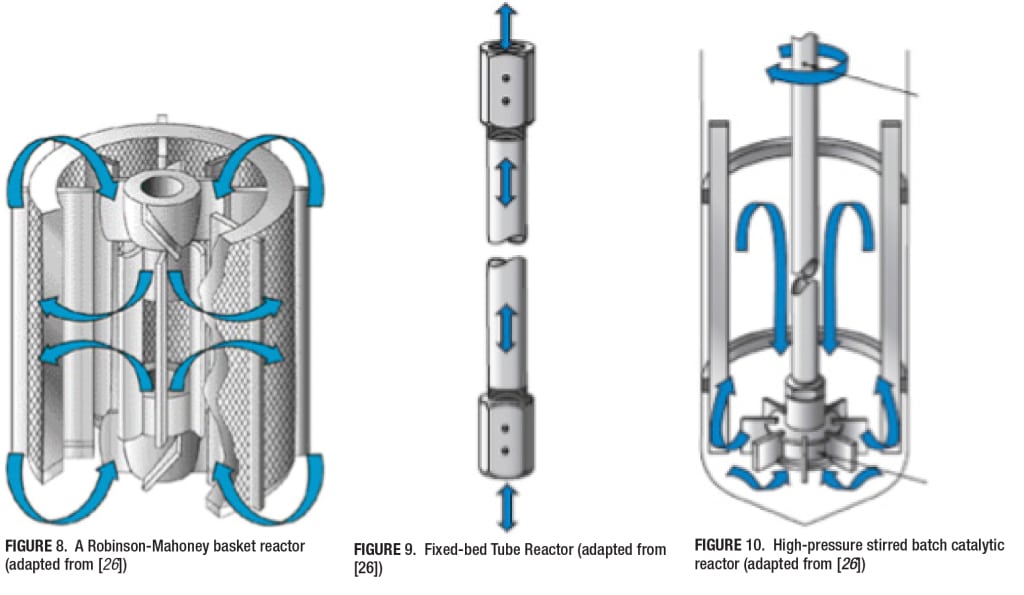
Choice and selection of a laboratory reactor. A proper choice for the laboratory catalytic reactor often is governed by the process characteristics. For example, if the experimenter is trying to run reactions with relatively fast kinetics or trying to simulate continuous processes, a good choice is the continuous tube-based fixed-bed reactors. If the kinetics of the reaction are relatively slow, a proper choice is either the Berty or the Carberry reactor. For three-phase reactions, where a liquid is a dominant phase (for instance, as a process solvent), or with an unsupported catalyst, an ideal choice is a high-pressure stirred autoclave batch system. For three-phase reactions with a supported catalyst, a Robinson-Mahoney catalyst basket reactor is an ideal choice.
Ideal flow. Regarding ideal flow, it is essential that ideal flows (plug or perfectly mixed flow) be assured in the laboratory reactor design and operation. The two flow patterns (plug flow and perfectly mixed flow) are called ideal because they enable a simple mathematical description and easy data analysis. In plug-type flow, the fluid moves over the catalyst in the form of plugs, and the flow is turbulent. This type of flow generally ensures the absence of temperature, velocity and concentration gradients, in the radial direction.
Perfectly mixed flow includes recycle reactors with a high recycle ratio and continuous stirred-tank reactors. Usually, deviation from ideality occurs because of the presence of gradients (due to incomplete mixing in a CSTR or axial mixing, wall effects or catalyst bypassing in plug flow). These gradients should be avoided in laboratory reactors, to ensure ideality.
Isothermal conditions. Isothermal conditions are very important from the standpoint of data analysis for intrinsic kinetics. Operation of the laboratory reactor under low conversions or differential conditions, dilution of the feed with an inert, dilution of the catalyst bed with an inert such as SiC, are typically some measures taken to ensure isothermality. Where possible, one can also use a process solvent (typically a high-boiling organic solvent) to absorb the exothermic heat of the reaction.
For bench-scale studies, one also needs to have very accurate measurements of temperature, and well-placed, sensitive probes (thermocouples) are thus necessary. For example, in a differential fixed-bed reactor, it is very important that the thermocouple is in close and intimate contact with the catalyst bed to avoid errors in the experimental data. Temperature is the single most important variable affecting the reactant conversions and product selectivities, especially for gas-solid catalytic reactions with high apparent activation energies. For example, the apparent activation energy for the synthesis of ethanol from a mixture of CO and H2 is about 100 KJ/mol.
Catalyst stability. The nature and extent of catalyst deactivation is also pivotal from the standpoint of the choice of laboratory reactors. If the deactivation is fast, a transport reactor (a reactor in which the catalyst particles are entrained in the fluid) is the clear choice, since the reactor residence times are short. For slow deactivations, a differential fixed-bed reactor (single-pass or recycle) is the proper choice.
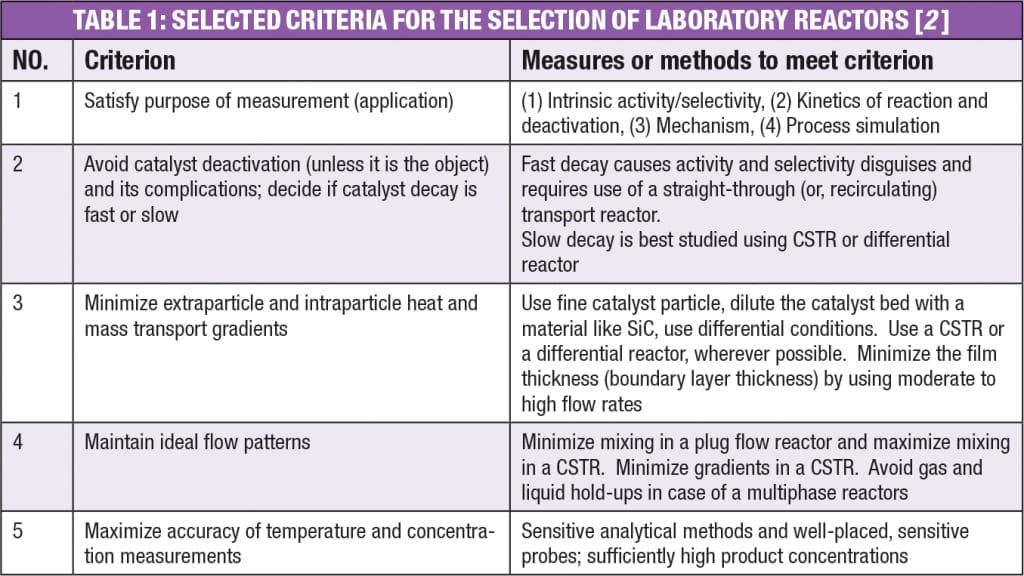
A how-to guide for selection of ideal laboratory reactor for catalytic studies is given in Table 1.
The discussion on intraparticle and extraparticle transport gradients warrants an in-depth treatment, which is too lengthy to include here. A classification of the laboratory reactors is given in Figure 4.
![Figure 4. A classification scheme for laboratory reactors (adapted from [3])](https://www.chemengonline.com/wp-content/uploads/2015/03/46.jpg)
Figure 4. A classification scheme for laboratory reactors (adapted from [3])
Reactors for gas-solid and liquid-solid reactions
Most assessments of catalyst activity in laboratory reactors are carried out in steady-state, fixed-bed microreactor systems, operated in a continuous flow mode. A schematic diagram of the typical fixed-bed microreactor system is given in Figure 5 [19]. In these laboratory reactors, a catalyst charge is placed at the center of a reaction tube, and the charge is held in place between two quartz wool plugs. The porous catalyst may be diluted with an inert material like SiC to improve heat transfer. A thermocouple is placed in close proximity to the catalyst charge at the exterior surface of the reaction tube, or in a thermowell (or, a sleeve) provided inside the tube. The flowrate of the reactants to the reactor is controlled using mass flow controllers. An inert material may be placed before and after the catalyst bed. The fixed-bed reactor can also be used in a cocurrent downflow mode for gas-liquid or gas-liquid-solid reactions. This mode of operation is frequently called a trickle-bed.
![Figure 5. A fixed-bed flow reactor has flow through a section of the catalyst bed, as seen in the inset (adapted from [19])](https://www.chemengonline.com/wp-content/uploads/2015/03/54.jpg)
Figure 5. A fixed-bed flow reactor has flow through a section of the catalyst bed, as seen in the inset (adapted from [19])
A classification of the tubular (fixed-bed) reactors based on size is as follows [11]:
Laboratory: 0.5 cm diameter tubular microreactor (0.1–1.0 g catalyst)
Bench: 2.5 cm diameter by 30–50 cm long tubular reactor (50–200 g catalyst)
Pilot: 7.5 cm diameter by 6–10 m long tubular reactor (20–100 kg catalyst)
Plant: 1–6 m diameter by 20–50 m long tubular reactor (20–100 tons)
A variant of the fixed-bed reactor is called the fluidized-bed reactor, where the catalyst bed is “fluidized” by the use of reactant gas flowing upward through a porous metal plate. At moderate-to-high gas velocities, the bed volume increases considerably, and the gas bubbles are no longer visible. Particle carryover to the reactor exit is avoided by operation at gas velocities lower than the entrainment velocities. This type of reactor circumvents the problems of pressure drop in the fixed-bed configuration, and is also more suited for exothermic reactions, due to the pseudo-homogeneous nature of the bubbling fluidized bed. It should be stressed, however, that the fluidized-bed reactors are more suited for industrial applications rather than studies at the laboratory scale.
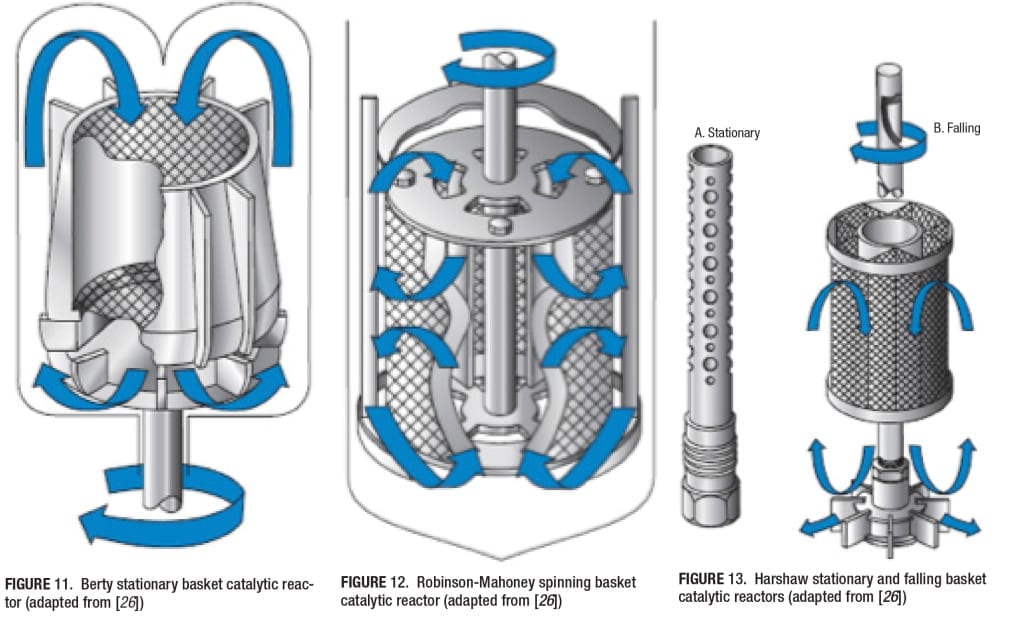
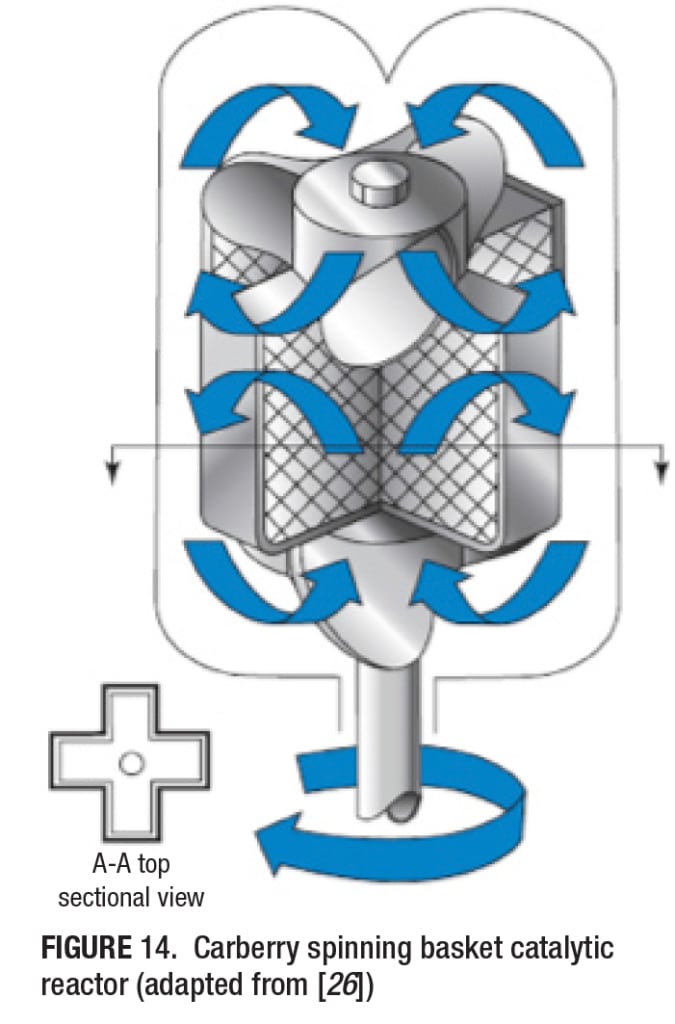
The fixed-bed reactors can also be operated with internal or external recirculation of the fluid, to approach “gradientless” reactors, for gas-solid or liquid-solid reactions. The different approaches possible for internal or external recirculation are given in Figure 6. In the Carberry reactor, the catalyst is placed in baskets and is rotated at high speeds. In the Berty reactor, the reactor fluid is forced past the catalyst at high speeds. That is, it is internally recirculated at high speeds. In a third variant, the fluid (gas or liquid) is externally circulated past the catalyst, using a suitable pump. As a major problem with these reactors is the gas-solid contact, two different designs of the Carberry reactors have been proposed, as shown in Figure 7.
![Figure 6. Two types of continuous stirred-tank reactors for heterogeneous catalysis (adapted from [3])](https://www.chemengonline.com/wp-content/uploads/2015/03/64.jpg)
Figure 6. Two types of continuous stirred-tank reactors for heterogeneous catalysis (adapted from [3])
Reactors for gas-liquid-solid reactions
![Figure 7. Basket designs for Carberry-type reactors: (a) flat blade; (b) pitched blade (adapted from [3])](https://www.chemengonline.com/wp-content/uploads/2015/03/74.jpg)
Figure 7. Basket designs for Carberry-type reactors: (a) flat blade; (b) pitched blade (adapted from [3])
Stirred autoclaves can be operated under unsteady-state conditions — that is, under batch or semi-batch conditions. These types of reactors are not suited for kinetic studies, where continuous-flow reactors are preferred. The batch and semibatch operation is more common in the fine chemical and pharmaceutical industries.
A popular gas-liquid-solid gradientless reactor is the Robinson-Mahoney stationary basket reactor, in which the gas-liquid dispersion is forced through the stationary basket (Figure 8). In this type of reactor, the fixed annular catalyst basket has baffles inside and outside to control vortices. The rotating shaft is equipped with two impellers that draw fluid into the center of the annulus at the top and bottom and outward through the catalyst bed. The gradient-free design and long-duration circulation capability for multiple phases has made the Robinson-Mahoney the most widely used design for supported, heterogeneous catalyst research with liquids. The gas-solid and gas-liquid-solid reactor designs can be summarized as follows:
Fixed-bed Tube Reactor (Figure 9) High-pressure Stirred Batch Catalytic Reactor (Figure 10) Berty Stationary Basket Catalytic Reactor (Figure 11) Robinson-Mahoney Spinning Basket Catalytic Reactor (Figure 12) Harshaw Stationary and Falling Basket Catalytic Reactors (Figure 13) Carberry Spinning Basket Catalytic Reactor (Figure 14)
Some advanced reactor and testing types including pulse reactors, temporal analysis of products (TAP) reactors, and steady-state isotopic transient kinetic analysis (SSITKA) are discussed elsewhere [19].
Most gas-solid catalytic reactions are accompanied by heat effects, thus, in addition to extraparticle and intraparticle diffusion, extraparticle and intraparticle heat transfer occurs. The presence of heat (temperature) and mass (concentration) gradients (Figure 10) confound the intrinsic kinetics of the reaction. The experimentalist must thus assure that the experiments are carried out in the absence of any transport gradients, to assure meaningful and reliable kinetic data from laboratory catalytic reactor system, that is amenable to scale-up. A followup to this article focuses on the transport gradients and heat and mass effects in catalytic reactions.
For further information, refer to additional works in the area [2026]. For novel reactor designs and future trends in catalytic reaction engineering, refer to [27-30].
Edited by Scott Jenkins
References
1. Perego, C. and S. Peratello, Catal. Today, 52 (1999) pp. 133-145.
2. Vannice, M.A., “Kinetics of Catalytic Reactions,” Springer, New York, 2005.
3. Kapteijn, F., J.A. Moulijn, in Handbook of Heterogeneous Catalysis, G. Ertl, H. Knozinger,F. Schuth, J. Weitkamp, Eds. Wiley-VCH, Weinheim, Germany, 2008.
4. Haider, M.A., M.R. Gogate, R.J. Davis, J. Catal., 261 (2009) pp. 9-16.
5. Gogate, M.R., R. J. Davis, Catal. Comm., 11 (2010), pp. 901-906.
6. Lee, S., A. Sardesai, Top. Catal., 32 (2005) pp. 197-207.
7. Lee, S. Methanol Synthesis Technology, CRC Press, Boca Raton, Fla., 1990.
8. Ko, M., S. Lee, Energy & Fuels, 1 (1987) pp. 211-216.
9. Ko, M., Mass Transfer Study in Liquid Phase Methanol Synthesis Process, Ph.D. Dissertation, The University of Akron, 1987.
10. Gogate, M.R., A Novel Single-Step Dimethyl Ether Synthesis Process from Syngas, Ph.D. Dissertation, The University of Akron, 1992.
11. Davis, M.E., R.J. Davis, “Fundamentals of Chemical Reaction Engineering,” McGraw-Hill, New York, 2003.
12. Bartholomew, C.H., R.J. Farrauto, “Fundamentals of Industrial Catalytic Processes,” John Wiley and Sons, 2006.
13. Ribeiro, F.H., A.E. Schach von Wittenau, C.H. Bartholomew, G.A. Somorjai, Catal. Rev. – Sci. Eng., 39 (1997) 49-76.
14. Cortright, R.D., J.A. Dumesic, Adv. Catal.,46 (2001) pp. 161-264.
15. Fogler, H.S., “Elements of Chemical Reaction Engineering,” Prentice-Hall, Englewood Cliffs, NJ, 1999.
16. Levenspiel, O., “Chemical Reaction Engineering,” John Wiley and Sons, 1999.
17. Dumesic, J.A., D.F. Rudd, L.M. Aparicio, J.E. Rekokse, A.A. Trevino, “The Microkinetics of Heterogeneous Reactions,” American Chemical Society, Washington, D.C., 1993.
18. Rostrup-Nielsen, J., J. Mol. Catal. A: Chem., 163 (2000) pp. 157-162.
19. Ross, J.R.H., “Catalytic Reators and Measurement of Catalyst Kinetics, in Heterogeneous Catalysis,” Elsevier B.V., 2012.
20. Weekman Jr., V.W., AIChE J., 20 (1974) pp. 833-870.
21. Doraiswamy, L.K., D.G. Tajbl, 10 (1974) 177-219.
22. Mahoney, J.A., NATO Adv. Stud. Inst. Ser. E, 1981.
23. P. Harriott, “Chemical Reactor Design,” Marcel-Dekker, Inc., New York, N.Y., 2003.
24. Moulijn, J.A., A. Tarfaoui, F. Kapteijn, Catal. Today, 11 (1991) 1-12.
25. Ranade, V.V., J. Chem. Sci., 126 (2014) pp. 341-351.
26. Catalytic Reactor Selection Guide, at www.autoclaveengineers.com/ae_pdfs/CR_Catreact_SelGd.pdf
27. Arakawa, H. et al. (with 34 co-authors), Chem. Rev., 101 (2001) 953-996.
28. Dudukovic, M.P., Catal. Today, 48 (1999) 5-15.
29. Dautzenberg, F.M., M. Mukherjee, Chem. Eng. Sci., 56 (2001) pp. 256-267.
30. Dudkovic, M.P., F. Lairachi, P.L. Mills, Catal. Rev. Sci. Eng., 44 (2002) pp. 123-246.
Authors
Makarand R. Gogate (259 Samarthnagar, Oppo. SBI Branch, Varad Ganesh Mandir Road, Aurangabad, 431 001 India; Phone: +91-99215 48705 Cell; Email: [email protected]) has over 15 years of practical, hands-on work experience in both academia and industry. His areas of expertise are experimental heterogeneous catalysis, materials chemistry and process design, as applied to the synthesis and characterization of nanomaterials and nanocomposites as well as applications in catalysis, synthesis gas conversion to higher-value chemicals, and biomass conversion and biofuels. An area of particular expertise is the design, assembly and operation of bench-scale catalytic reactor systems, including fixed-bed and slurry reactor systems (batch, semibatch, and continuous), for reactivity studies and reaction kinetics. Gogate has been a researcher, lecturer and project engineer, and has published numerous peer-reviewed articles and has received four patents. He received a Ph.D. from the University of Akron and a B.S.Ch.E. from the University of Mumbai.