When faced with the complexity of predicting powder flow, it is tempting to reduce a material’s flow behavior to a single number or even a flow function. The method presented here, however, compiles a number of relevant parameters into a diagram that is easy to interpret
Accurate prediction of particulate-solids flow behavior during storage and feeding has eluded all but the most experienced solids handling experts. Often the process engineer is faced with the awkward task of making sense of bulk behavior. A powder sample held in a jar may appear to be free flowing, but hammer rash — jargon for the practice of hitting hoppers with pipes to dislodge powders in the hopper — is evident in many plants, suggesting a different story (Figure 1).

If truth be told, the interaction of material characteristics, equipment design and interfacing, flow regimes and operational circumstances play roles that rival the significance of powder testing results. Perhaps the most meaningful parameters that affect plant performance are how the material slides against a contact surface, the material’s shear strength and how the bulk density, itself, varies. Note that all of these factors are often affected by the compaction and stress conditions imposed.
As ever, when faced with complexity it is tempting to reduce a powder’s flow behavior to a single number or even a flow function. However this inevitably gives limited insight into a material’s bulk performance. In this article, the author, based on a joint paper with Don McGlinchey of Glasgow Caledonian University presented at the 7th World Congress of Chemical Engineering [1], presents a better way of interpreting powder characteristics to aid in the prediction of bulk solid flow.
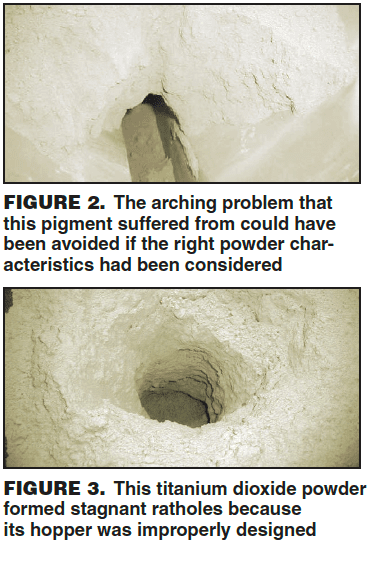
Every industrial sector — petrochemicals, plastics, bulk and fine chemicals, pigments, agrochemicals and detergents included — is involved in handling bulk solids in either raw-ingredient form, intermediate processing or right up to the point of sale. A prodigious variety of bulk solids are stored in hoppers or silos in quantities ranging from a few kilos to hundreds and, in some cases, thousands of tons. Unfortunately, many installations, regardless of their size, suffer from unreliable flow caused by the contents forming stable arches (Figure 2) and ratholes (Figure 3).
Even a plant that has historically operated well can develop problems as a consequence of formulation and raw-feed changes. Assessments of a bulk solid’s flow properties are, therefore, important features of plant design and problem solving.
Powder testing for flow
Two main characteristics are important for flow: (1) how the product slips on a contact surface (wall friction) — product has to slide down the walls of a hopper or along the flight of a screw — and, (2) the resistance offered by the powder bulk to deformation/flow (shear strength) — arches and ratholes form when the material develops sufficient strength. These characteristics are influenced by the condition or compaction of the bulk because a tightly packed bed is less free flowing than a loose aerated powder. This condition is directly related to the bulk density. In hoppers the stress influences the bulk density.
Consequently, wall friction, shear strength and bulk density are three properties of bulk solids that need to be measured to design for mass flow in a hopper and avoid arching at the outlet. Mass flow brings a number of benefits — for example, reducing segregation — and offers the best approach for flow towards the outlet. Even non-mass-flow hoppers require a flow channel sufficiently large enough to destabilize any rathole that may form and a wall angle steep enough to self-clear if it is to function well.
Characterization of bulk solids
Predicting the behavior of bulk solids in every case has led some to look for a single number to use as a guide to flow. This reductionist approach, however, is fraught with problems. For example, there is no obvious reason why a bulk solid that has high friction should also have a strong cohesive tendency or vice a versa. So, while the situation may worsen for flow when both these features are present, they are not necessarily related.
A better approach to predicting flow behavior is to take the characteristics of wall friction (φw). shear strength (σf), bulk density (ρb) and add three further factors: hopper wall angle (βc), outlet size (Dcrit) and Hausner ratio (H.R.; the ratio of tapped bulk density to loose bulk density; where the greater the ratio, the more sensitive the powder is to the way it is handled). Using these factors, we can produce a ‘spider’ diagram.
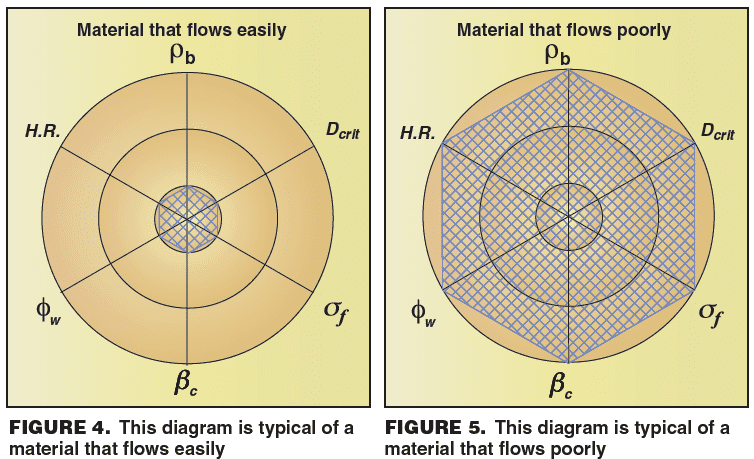
To produce the diagram, a series of three concentric circles are divided by axes for each of the characteristics. These axes intersect with the smallest diameter circle, where that particular characteristic describes ‘easy flow,’ with subsequent bigger diameter circles defining ‘modest’ and ‘poor flow.’ Two idealized situations can then be presented for an ‘easy flow’ material (Figure 4) and a ‘poor flow’ one (Figure 5), with the shaded ‘web’ detailing the particular characterization attributes.
The spider web diagrams can be more than qualitative if the data from the tests on 150 different materials with a very wide range of flow behaviors is used to define the ‘easy’, ‘modest’ and ‘poor’ flow circles (Table 1).

Note that the bulk density axis is the reverse of the others because decreasing bulk density usually means poorer flow. A practical example to justify this assertion is that most milling operations lower bulk density and worsen flowability of powders when they are stored.
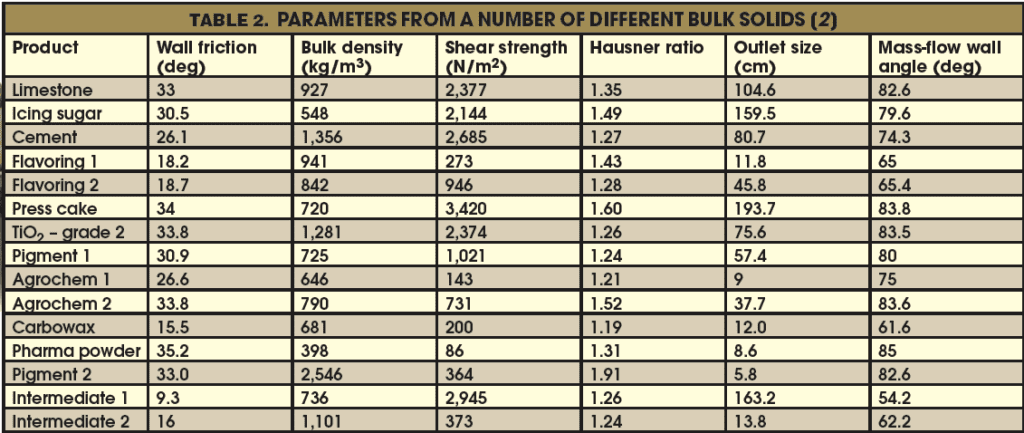
A selection of bulk solids with their measured and derived data is presented in Table 2.
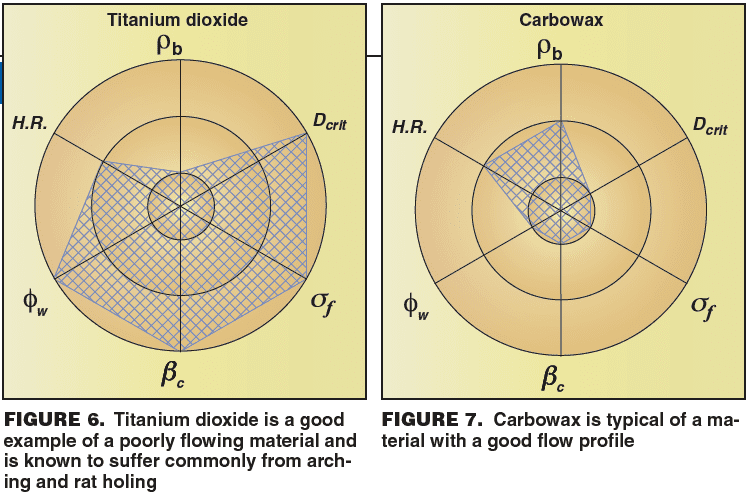
To show the usefulness of the spider diagram as a data handling technique, diagrams are constructed for a particular grade of titanium dioxide (Figure 6) and carbowax (Figure 7). Titanium dioxide is a good example of a poor-flow material that commonly suffers from arching and ratholing. Another material, carbowax, closely follows the idealized good-flow material profile that is confirmed by practical experience.
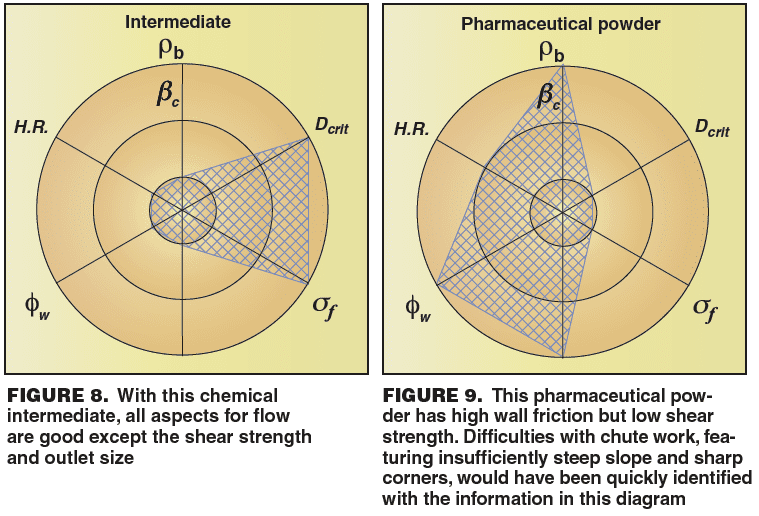
Two other examples highlight how this multi-parameter approach is advantageous. Figure 8 shows the resultant diagram for a material designated as Chemical Intermediate 1. All aspects for flow are good in this case except the shear strength and outlet size. Indeed, a practical application for batch handling of this material required invertible bins that upset the consolidation of the material in order to ensure reliable flow to the process.
Meanwhile, the pharmaceutical powder illustrated in Figure 9 has high wall friction but low shear strength. Difficulties with chute work, featuring insufficiently steep slope and sharp corners, would have been quickly identified with the information in the spider diagram. The necessary attention might, then, have been directed towards examining the effects of surface finish and using corners of a more generous radius as practical solutions.
Conclusion
In conclusion, a novel spider diagram integrating the measured wall friction, shear strength, bulk density, and three calculated parameters [hopper wall angle, outlet size (shear strength/bulk density ratio) and Hausner ratio], offers a more rounded and direct picture of flow characteristics. Exciting prospects for this method include comparison between different grades of the ‘same’ material and refining of the scales of the axes to provide greater sensitivity.
The technique incorporates hopper-design criteria and thereby offers the possibility to fine tune axes scales to suit experience with particular plant/product combinations. The author acknowledges that there are many aspects that affect bulk-flow behavior. Refinement of this approach to include other factors such as internal friction, lateral stress ratio and increased definition in scale, can only improve the chemical engineers ability to match plant performance /design to bulk solids characteristics for reliable handling.
Edited by Rebekkah Marshall
