Bigger is better. That simple statement summarizes one of the fundamental principles of chemical engineering. It is a statement that we frequently want to ignore, but if capital efficiency is the main concern, it is always true. All engineers need an occasional reminder of this truism and can be aided by a tactile exercise that shows the inescapability of the bigger-is-better mentality. Origami, the traditional Japanese art of paper folding, provides a simple means to illustrate that bigger truly is better in cases where the capital efficiency of containing and moving material is the critical parameter.
Practical solutions define engineering
Engineering seeks to harness the fundamental laws of nature to do something useful and, at its best, something that is practical. For something to be practical it has to work well and it must be economical when compared to other ways of obtaining the same result. Chemical engineers are bound first and foremost by the laws of heat and mass balance. These are part of the physical laws that place clear limits on what is possible. Engineers are left to wrest practical solutions from the options that are allowed by physical laws. Practical chemical processes must be economical, operable and reliable, whereas no hard and fast laws govern economics, operability and reliability.
 |
 |
 |
 |
 |
 |
Economics, and especially the economics of scale, don’t strictly follow absolute rules. Some, in fact, have argued that the laws of economics are always changing [1]. A simple origami example can be used to describe one part of the chemical engineering economic puzzle: unit capital cost. Unit capital cost is the cost to manufacture a vessel divided by the capacity of the vessel. A vessel can be a tank, hopper, reactor, pipe system, cart, truck, ship, barge or anything that holds “stuff.” Just as in origami, most vessels begin as flat material that is formed and fabricated.
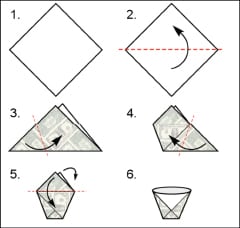
The simple origami cup
Figure 1 shows the six steps required to fashion an origami cup. It is one of the simplest containers that can be made from a sheet of paper with only folding, yet is robust enough to actually withstand being filled with a liquid. It begins, like most origami, with a square sheet of paper. It is shown assuming that one side of the paper is blank and the other patterned. The pattern shown is slightly distorted images of currency to stress that the amount of material used in fabrication is proportional to the cost of the material.
Figures 2 and 3 show how to convert a sheet of normal letter-sized paper, 8.5 by 11 in., into sheets of paper useful for this demonstration. Figure 2 creates a square 8.5 by 8.5 in. Figure 3 creates four squares one-fourth the area of Figure 2 (4.25 by 4.25 in).
Begin by folding the larger sheet as shown in Figure 1. When you get to step 6, spread the top and bottom of the cup to as close to circular as possible. This gives a paper cup with a volume of approximately one cup or 14 7/16 in3.
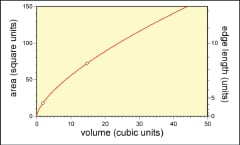
Doing the same operations with the smaller square of paper creates a smaller cup. The volume of this paper cup is only about one-eighth of a cup or about 1.8 in3. The area of the paper sheet used is plotted as a function of cup volume in Figure 4. Measured cup volumes are a surprisingly good fit to a power law where the area of the paper used changes as the volume contained in the origami cup to the two-thirds power
The amount of effort invested in making the origami cup doesn’t change with the size of the paper. To make a number of little cups that would hold as much as the big cup, seven more little cups would have to be folded. Holding the same amount of material requires twice as much material and eight times more work when little cups are used. The analogy to processing industries is that the cost of a vessel is dominated by the cost of the material and the cost of the labor. The cost per unit volume of the bigger cup will be lower than the little cup. Just as making the larger paper cup was more efficient in terms of both labor and materials, the fabrication of a metal vessel is more efficient in materials and labor as the vessel gets larger.
Derivation of the power law
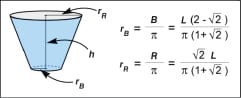
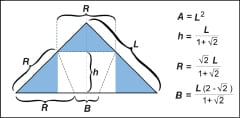
In this simple example, a flat sheet of paper is folded to approximately form a truncated cone. The critical dimensions used in folding the cup are shown in Figure 6. L is the width of the paper square used to fold the cup. The area of the paper used, A, is simply the square of the width. R is the length of the edge that will become the rim of the cup and B is the length of the folded edge that becomes the base of the cup. Finally, h is the height of the cup. Sheet area, R, B and h are all functions only of the width of the paper used.
The truncated cone formed has the dimensions shown in Figure 5. The volume contained is a function of the rim radius, rR, the base radius, rB, and the height. All of these values can be shown to be determined solely by the width of the paper used to make the cup. Calculation of the volume, therefore, yields an expression that is solely dependent upon the size of the paper used. Area is simply the square of the width, so volume can be expressed interchangeably as a function of the sheet area or as a function of the sheet width.
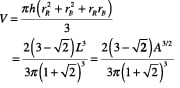 |
(1) |
Rearranging this expression and calculating the value of the constant yields:
| (2) |
Figure 4 shows this equation plotted. Area, as previously noted, is proportional to cost of the material required for the cup and volume is the capacity or scale. The cost of material scales as the volume to the two-thirds power in the simple origami cup, just as it commonly does in the construction of tanks, vessels, piping and other chemical engineering units. The capital requirement divided by the volume gives you the capital efficiency. The simple origami cup illustrates that when constructing a vessel, the “bigger-is-better” ideology always applies. The origami cups show that the capital efficiency goes up as the size goes up. All other things being equal, this means that larger vessels will require less capital per unit of product and will, therefore, inescapably produce product at lower cost.
Implications
The relationship between the benefits of increasing scale and its behavior with respect to the relationship between surface area and volume has been previously noted [2]. In both cylinders of increasing radius and spheres, the surface area increases as the volume increases to the two-thirds power, just as demonstrated with the simple origami cup. Measurement of the actual cost of fabrication as a function of scale has validated the 2/3 engineering scale coefficient [3, 4]. All available data suggest that processing plants in the process industries are moving to larger and larger scales [5, 6, 7]. It is well established that production costs drop as market size grows [8, 9], yet the belief that bigger is better is still commonly questioned.
Many would have us believe that certain plants can be made at small scale and remain competitive with larger, conventional chemical and fuels facilities. Comparisons are made to Moore’s law [10], indicating that rapid technology change is possible. Moore’s law is actually not so much about change, as it is about making things small. Moore’s law is about the pace of miniaturization. Moore’s law hasn’t actually shown indications that it applies in the macro world. Automobile fuel efficiency hasn’t followed a Moore’s law improvement. Efficiency of gas turbines hasn’t followed Moore’s law. Efficiency of distillation hasn’t followed Moore’s law. Moving mass dominates much of the processing cost. Mass can’t be miniaturized. The chemical industry is not alone in benefitting from economies of scale. The milk [11], poultry [12], shipping [13] and biofuels [14] industries have all benefited, just to name a few. These are all industries where the material supply ultimately limits the scale due to rapidly increasing transportation costs as the radius of collection increases.
Wright first noted that airframe costs decrease as a power law of the cumulative production [15], effectively noting what is commonly known as the learning or experience curve. The logic follows that if you simultaneously produce three units, the labor cost would roughly equal the cost to build two independently. Efficiency is gained through experience and learning. Simply stated, Wright’s law states that cost per unit decreases as more units are made. Efficiencies do come through mass production, as Henry Ford and others clearly have demonstrated. The reduction of cost as production goes up is one of the only options for improving upon the benefits to capital efficiency due to scale. Those that indicate they will make cost-effective processing plants in shipping containers [16] can only do so if they make many identical plants.
There are clearly reasons why larger doesn’t always work, but pure capital efficiency is not one of them. A limited market or accessibility to feedstock can limit the scale of operation. Such limitations preclude going to ever-larger scale in a single plant and, therefore, make options like mass production a practical way to optimize cost of production. However, mass production as a way to improve capital efficiency has some issues. No individual has the capacity to simultaneously fabricate more than a few items, meaning that a point of diminishing returns can develop relatively quickly. To make more, a second person must be hired and the economies now increase on the basis of the incremental amount an individual can produce. The larger issue is that mass production does not preclude making each item even infinitesimally bigger. Those infinitesimally bigger plants will have an advantage over the smaller plants, even though fewer will be made. Early in the adoption cycle, the larger facility is favored, even before the benefits of mass production are realized. Discussion of favorable nth plant economics ignores the fact that plants 1 through n still need to be economically attractive or they won’t get built.
 |
Automobile manufacturing is one of the best examples of mass production. Over 6 million light trucks were produced in North America in 2012. Yet, as Figure 7 shows, scale wins over the experience curve [17]. Mining trucks, the largest trucks that are made, and pickup trucks largely perform the same task. The mining truck will haul 350 cubic yards, while the pickup hauls only about two and three-quarter cubic yards. That means that it would take somewhere between 125 and 200 pickups to do the same job as the mining truck. Clearly, mine operators would choose pickups if the economics worked out. Even with a price tag in the millions, the big truck is more efficient both in terms of capital and labor. It is a good picture to recall when mass production is touted as a means to overcome economies of scale.
Final remarks
The origami cup reinforces the chemical engineering two-thirds scaling rule. Chemical plants are all about holding stuff — they are about containing and moving volumes of material. Despite common misconceptions, it is nearly impossible to beat going bigger, whether it be high-tech or low tech. Scale simply wins when material is being handled.
References
1. Drum, Kevin, The Laws of Economics, Mother Jones, 19 May 2011.
2. Moore, Frederick T., Economies of Scale: Some Statistical Evidence, Quarterly Journal of Economics, 73(2), May 1959, pages 232–245.
3. Remer, D. S., and Chai, L., Estimate Costs of Scaled-up Process Plants, Chemical Engineering 94, no. 7 (1990): 138–175.
4. Brown, T.R., Capital Cost Estimating, Hydrocarbon Processing, October 2000, pages 93–100.
5. Lieberman, Marvin B., Market Growth, Economies of Scale, and Plant Size in the Chemical Processing Industries, Journal of Industrial Economics, 36(2), December 1987, pages 175–191.
6. Buffenoir, M.H., others, Large ethylene plants present unique design, construction challenges, Oil and Gas Journal, 19 January 2004, pages 60-65.
7. Parin, M., and Zugarramurdi, A., Investment and Production Costs Analysis in Food Processing Plants, International Journal of Production Economics 34, no. 1 (1994): 83–89.
8. Szmant, H. Harry, “Organic Building Blocks of the Chemical Industry,” John Wiley and Sons: New York, 1989, page 8.
9. Nagy, Bela, others, “Statistical Basis for Predicting Technological Progress.” arXiv preprint arXiv:1207.1463 (2012).
10. McAdams, Mike; Wrong Message, Wrong Time, Biomass Magazine, 24 October 2011.
11. Shields, Dennis A.; “Consolidation and Concentration in the U.S. Dairy Industry”, Congressional Research Service Report, 27 April 2010.
12. Ollinger, Michael, others, Poultry Plants Lowering Production Costs and Increasing Variety, Food Review, USDA Economics Research Service, May–August 2000, volume 23, Issue 2, pages 2–7.
13. Landauro, Inti; Container Ships Bulk Up and Slow Down, The Wall Street Journal, 30 December 2012.
14. Van Den Wall Bake, J. D., others, Explaining the Experience Curve: Cost Reductions of Brazilian Ethanol from Sugarcane, Biomass and Bioenergy, Vol. 33, no. 4 (2009): 644-658.
15. Wright, T.P., Factors Affecting the Cost of Airplanes, Journal of Aeronautical Sciences, Vol. 3, No. 4 (1936), 122-128.
16. Investing in Future Transport, Cleantech Investor Magazine, July 2012,Vol. 6, issue 4, page 10.
17. Banholzer, W.F., and Jones, M.E., Chemical Engineers Must Focus on Practical Solutions, AIChE Journal 59(8) 2013, 2708-2720.
Author

Mark E. Jones is executive external strategy and communications fellow for The Dow Chemical Company (2020 Dow Center, Midland, Mich. 48674; +1-989-636-4307; Email: [email protected]). Jones joined Dow in 1990 and has held many technical positions in research and development during his tenure at Dow. In his current role, he assists the chief technology officer with technical assessments and development of external communications. He also provides technical support for Dow’s Renewable Chemistries Expertise Center. He spent most of his career developing catalytic processes. Jones holds a B.S. in Chemistry from Randolph-Macon College and a Ph.D. in Physical Chemistry from the University of Colorado-Boulder.